Law of Sines

Law of Sines

1st Method To Solve The Law Of Lines

The sides of the triangle are proportional to the lines of the other opposite angles.

Law of Sines

Exercises

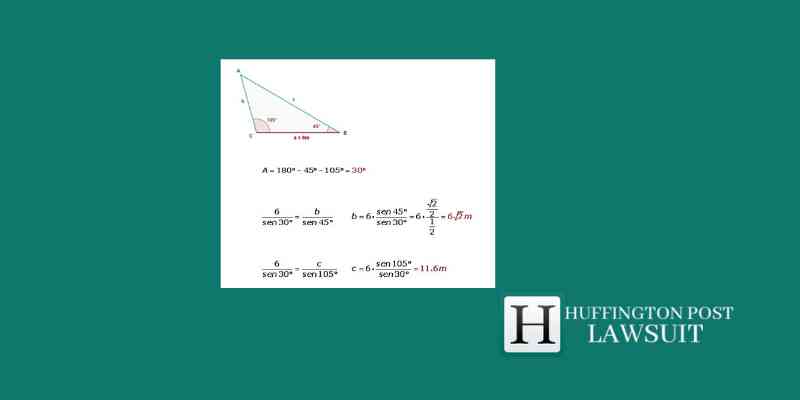
From a triangle we know that: a = 6 m, B = 45 ° and C = 105 °. Determine the remaining elements.

Law of Sines

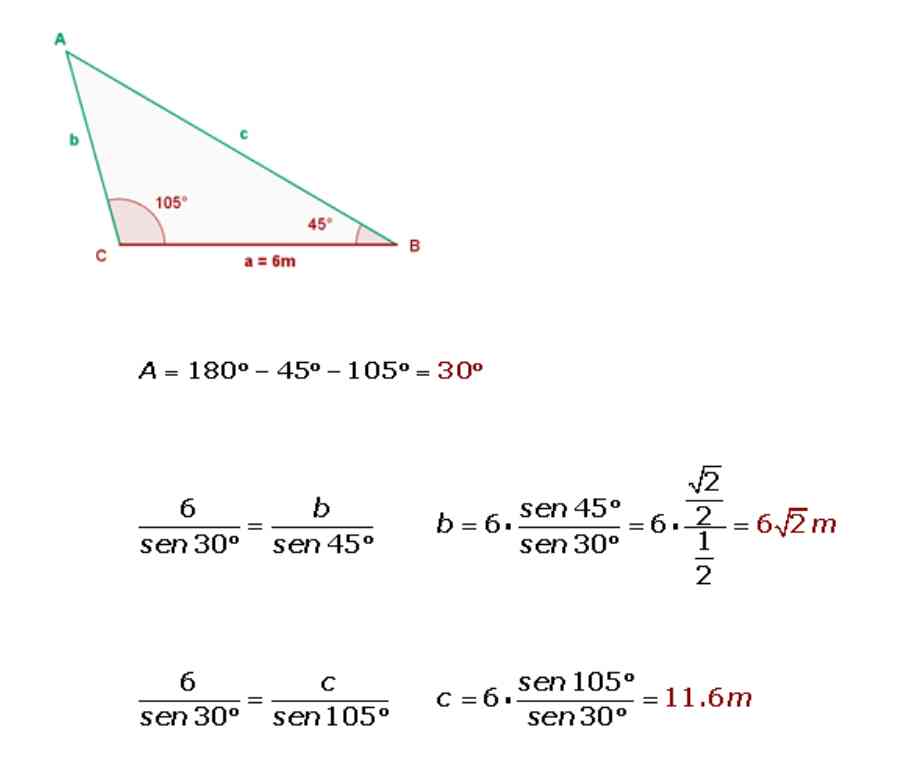
Find the radius of the circumscribed circle in a triangle, where A = 45 °, B = 72 °, and a = 20m.

Law of Sines

Theorem or law of cosine

At a triangle the square of each side is equal to the sum of the squares of the other two minus the double product of the two times the cosine of the angle they form.

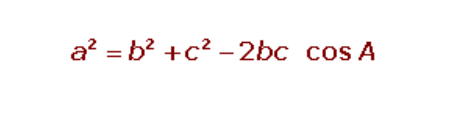
Law of Sines

Examples

The radius of a parallelogram measure 10 cm and 12 cm, and the angle they form is 48 ° 15 ‘. Calculate the sides.

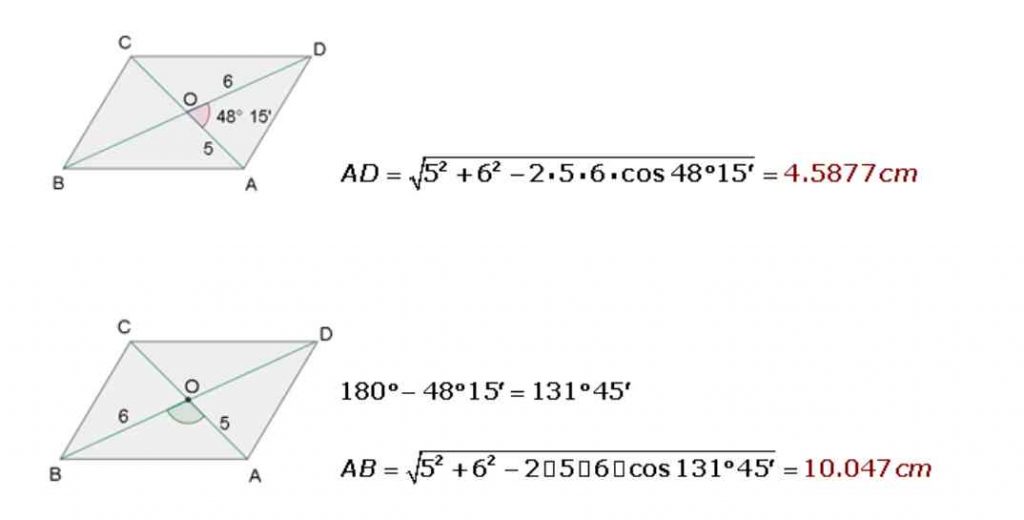
Law of Sines

The radius of a circle is 25 m. Calculate the angle which the tangents will make to said circumference, drawn by the ends of a rope of length 36 m.

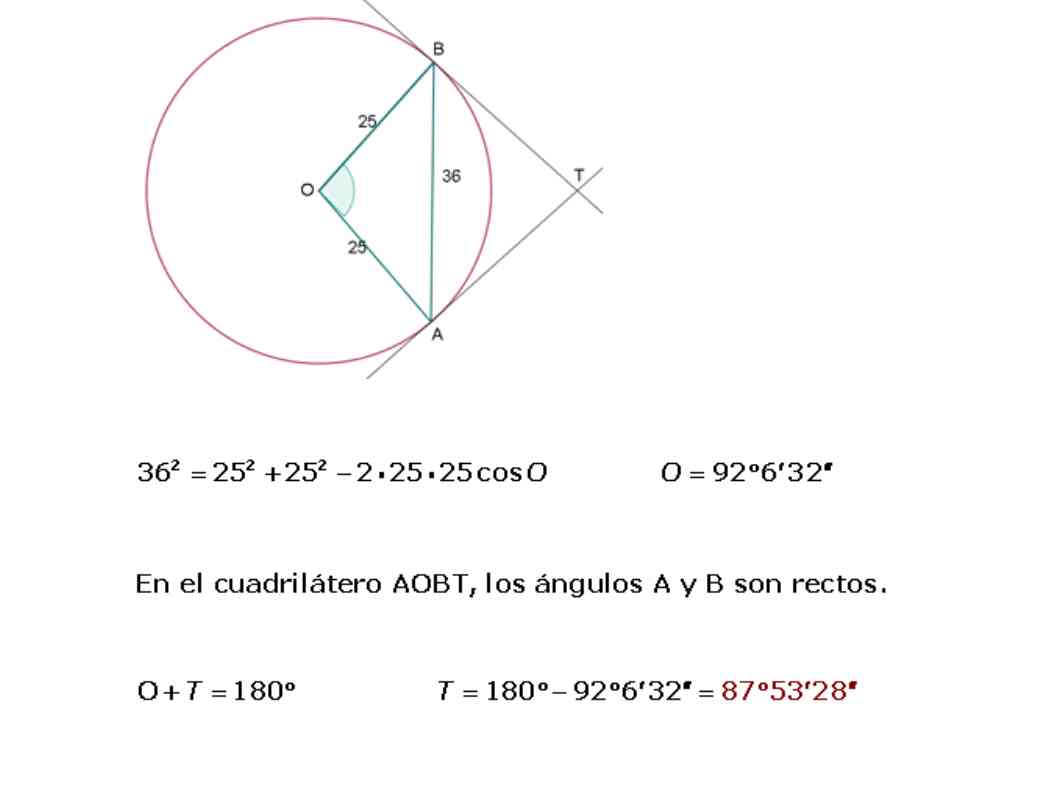
Law of Sines

Theorem or law of tangent

If A and B are angles of a triangle and their corresponding sides are a and b, it follows that:

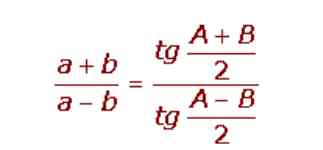
Law of Sines

You will learn how to solve oblique triangles by applying the law of sines.

Thus far, we have solved the right triangles. However, it is also common to find issues with triangles that aren’t rectangles, such as acute angles or obtuse angles. To solve these problems, the method we’ve used does not work, but we may use the law of sines.

2nd Method To Solve the Law of Sines

For any triangle in the plane, together with inner angles, and opposite side spans respectively, it is fulfilled:

Quite simply, the law of sines states: for any triangle which lies within a plane, the lengths of its sides are proportional to the sines of its angles. When we know the length of one side of the triangle and its interior angles, we could compute the lengths of the other two sides employing this law.

Example 1

Solve the next isosceles triangle:

Considering that the triangle is isosceles, both sloping sides measure 3 cm. We will demonstrate it using the law of sines. For this, we define cm, and we will need to calculate. Using:

We can clear to get:

This demonstrates it is an isosceles triangle. To figure the period of the foundation, we have to mention that the amount of the two famous angles is and that the next pitch has to measure. With this, we can reuse the law of sines to Compute the length of:

Now we substitute the known values:

And with this, we’ve solved this severe triangle.

The sine law also works for obtuse triangles, as shown in the next instance.

Example 2

Solve the following obtuse triangle:

In this case cm, also we can calculate:

Now we can calculate the length of the side employing the law of sines:

Clearing and solving, we get a cm.

Finally, we could calculate the value of:

Substituting the values ​​we get:

And we completed it.

Breast law also serves to fix problems in a variety of contexts.

Example 3

A building business will drill a tunnel through a hill to decrease the transport time of Acatlán (a stage in the figure) into Bacatlán (point ). If the tunnel is on the line, which passes through the things and What will be the distance in the street? Cazatlán is your point indicated in the next figure. The following were measured: kilometers.

We start by imagining that we can calculate the angle value:

We can calculate the distance between the things and implementing the law of sines:

We can even calculate the distance between the point and Bacatlán:

With this, we have fully resolved the triangle. It follows that now to buy from Acatlán into Bacatlán they travel at least 31.6 kilometers from Acatlán to Cazatlán very first, then 42.4 km from Cazatlán into Bacatlán.total. With the new street that will pass through the tunnel, space is shortened to approximately 40 km.

Example 4

On the point there’s a plane which travels east, from there to levels north (left of the front of the plane) is an airport. If you go 100 km, the airplane is now located at the point, the airport itself is submerged from precisely the same plane. How far apart are the tips?

We begin by drawing a diagram to get a better idea of ​​this problem:

We specify: and. The third angle, why. To figure out the distances, we wish to know we apply the law of sines.

The space from the point until the purpose is:

And we’re done.

Example 5

Marco noticed that an angle of one point on the ground to the peak of a tree, but if you advance horizontally 20 meters towards the tree into a point, the angle that is formed is. What’s the height of the tree?

We begin by outlining the scenario:

Since the angles and are supplementary and measure, it follows the step. Now that we understand two interior angles of the triangle, we could calculate the angle measure:

We can apply the law of sines to calculate the action of this side:

We can calculate the length of the segment, employing the definition of the cosine function in the right triangle:

Finally, we can apply the Pythagorean theorem to the right triangle to figure out the height of the tree. In this triangle, the hypotenuse steps, along with the known leg, And we are done.